MD5(Message-Digest Algorithm 5,消息摘要算法第五版),是广泛使用的哈希算法之一,主流编程语言普遍已有MD5的实现。第一次接触是在写项目的时候,直接用PHP中的现有函数来加密一些信息。Web安全选修课中的一个作业是要实现这个算法,这里记录一下学习的笔记。
MD5的输入是一条不定长度的信息,输出一条固定长度128位的信息,也即生成四个32位数据。基本方式为,求余、取余、调整长度、与链接变量进行循环运算。
例如英语中的经典句子“The quick brown fox jumps over the lazy dog”,经过加密后,
MD5("The quick brown fox jumps over the lazy dog") = 9e107d9d372bb6826bd81d3542a419d6
算法过程
预处理,假设我们要加密的信息长度为B 字节,即一共为b = 8B位。
根据MD5的填充原则,我们需要补上1个1和n个0,令总位数除512的时候余448。
可以推出,经过第一步填补后的位数仍为8的位数,因此补上一个1后必定至少补七个0,相当于补上0x80.
然后我们一直在后面补上0x00,直到总位数除512时余448。
之所以要让余数刚好为448,是因为我们需要在后面补上用64位表示的原信息长度,448+64 = 512,恰好能让信息位数为512的倍数。
原信息长度为8B bit,我们将8B这个数字用2进制64位表示出来,然后通过小段规则(低字节在前)补到信息的末尾。
这样一来,我们有了一组增补后长度为512N的信息。
增补后的信息可以分为N个512位(64字节)的块,可以分为16个4字节大小的组,每组32位。
我们定义4个幻数,0x67452301,0xefcdab89,0x98badcfe,0x10325476,分别为A,B,C,D
以及4个非线性位操作函数
对每一块进行操作,接下来的64次循环,每16次都会用到其中一个函数。
对于每一个64字节的块,我们都算出其非线性函数的值,然后与A,该轮对应分组,以及一个数组K的对应值相加,然后进行一定的逻辑循环移位。
K数组大小为64,产生过程K数组的过程是:遍历这个数组,求出当前下标的sin绝对值与2的32次幂的乘积,再取整。
每次循环后,我们将A,B,C,D的值循环交换,即A的值赋给D,B的值赋给A,如此循环左推。对于每个64字节块都进行一次这样的操作,完成后A,B,C,D的值即我们加密后的信息,注意的是我们需要小端格式的输出。
源代码
Github链接
算法应用
接触种子下载的用户会注意到,BT软件会通过计算MD5检验下载到的文件片段的完整性。MD5作为一个哈希算法不可能没有碰撞。2009年,谢涛和冯登国破解了MD5的碰撞抵抗,该攻击在普通计算机上运行只需要数秒钟。因为这一碰撞风险,用户的密码加密算法不应采取MD5。改进MD5的方式可以是,在加密前,字符串加上一组随机字符串,只有双方才掌握这一随机串,这种方法可以防止通过碰撞来获得加密的内容。网上我们能搜到的MD5解密算法,原理便是通过对大量已有的字符串进行加密获得加密后的串,当用户需要解密的时候,才在其中寻找其原串。
2014年12月28日星期日
SOJ 1153 马的周游问题
题目描述
国际象棋棋盘中,马/骑士(Knight)行日字型,和中国象棋一样。给定一个马的起点位置,我们要求出马把棋盘中所有位置周游一遍并且不会出现重复的路线
对这样一个8 * 8的棋盘编号如下:
算法思想及解题用到的主要数据结构
本题中我们将会用到深度优先搜索+回溯的算法。对于马棋子的当前位置,我们找出它能够往下走的下一位置,从中选择一个位置走,当马无法找到新的可行位置,而问题又未解决(即棋盘未被周游)时,我们让它回溯到前一个状态,说明前一个选择的位置是一条死路。我们继续选择可行的位置,直到没有新的可行位置,我们回溯到前一状态。
在一个假设不限大小,所有位置都合法的棋盘,一个马棋子能够走八个方向,也即有八个可选的位置。对于一个马的位置状态,我们求解出所有这八个位置,然后通过合法性判断剔除出超出8x8范围的位置。同时,由于周游要求所有的位置只被寻访一次,我们建立一个布尔型数组记录已被寻访过的位置,并在每次选择前先将已被寻访的位置剔除。(一个8x8大小的布尔矩阵是64字节,我们可以用一个double类型的8字节(64位)来表示,通过位操作来改变这个记录)。但由于题目的棋盘范围为8x8,盲目地选择位置搜索仍然会带来不必要的时间耗损。
逐步求精算法描述
一条成功周游的路线,我们在找寻时假设有N个合法的next位置,我们假设所有的next位置会导向死路的概率相同,我们倾向于先搜索可行路径更少的节点,这样就能够及早地发现死路及早回溯。
如图,若在选择next节点前,我们先根据next节点的next节点个数进行升序排序,在通常情况下能够避免在找寻中在错误的路径中耗费太多时间,同时,一条可行的路径在搜索过程中,next节点的个数应该是越来越少的。
我们在position这个数据结构中添加一个变量potential记录这个位置的合法next位置的数目,在选择下一节点前,先通过排序,选择potential更小的节点进行访问。
上面的这个优化思路是可行的。为什么?
维基百科告诉我们,马的周游问题其实就是一个古老的图问题----哈密尔顿路径的一种形式.题目要求寻找的是一条“开路径”(遍历所有位置后不需要回到初始位置)。Cull和Conrad证明了对于任何一个m×n(m≤n且m≥5)棋盘,至少有一个(可能是开路径)的马周游路径。
上面我简单用图表示的现象,十分没有说服力,因为我也没办法确定这样一定正确。事实上,这个想法和Warnsdorff规则不谋而合。
Warnsdorff在1823年提出了一个启发性的贪心算法,我们称为Warnsdorff规则,指在所有可走且未经过的方格中,马只可能走这样一个方格:从该方格出发,马能跳的方格数最少;如果可跳的方格数相等,则从当前位置看,方格序号小的优先。依照这一规则往往可以找到一条路径但是并不一定能够成功。换言之,在进行深搜时优先拓展拥有最少下一步可能移动位置的子节点。
此外,Warnsdorff 算法还有两个改进版本 W+和 W2,但在8 × 8这样小规模的棋盘上
优化效果并不明显。这个问题可以通过分治法和神经网络来解决。
Further Read:Knight's tour - Wikipedia 下面的参考文献
国际象棋棋盘中,马/骑士(Knight)行日字型,和中国象棋一样。给定一个马的起点位置,我们要求出马把棋盘中所有位置周游一遍并且不会出现重复的路线
对这样一个8 * 8的棋盘编号如下:
01 02 03 04 05 06 07 08
09 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
从维基上盗个图
算法思想及解题用到的主要数据结构
本题中我们将会用到深度优先搜索+回溯的算法。对于马棋子的当前位置,我们找出它能够往下走的下一位置,从中选择一个位置走,当马无法找到新的可行位置,而问题又未解决(即棋盘未被周游)时,我们让它回溯到前一个状态,说明前一个选择的位置是一条死路。我们继续选择可行的位置,直到没有新的可行位置,我们回溯到前一状态。
在一个假设不限大小,所有位置都合法的棋盘,一个马棋子能够走八个方向,也即有八个可选的位置。对于一个马的位置状态,我们求解出所有这八个位置,然后通过合法性判断剔除出超出8x8范围的位置。同时,由于周游要求所有的位置只被寻访一次,我们建立一个布尔型数组记录已被寻访过的位置,并在每次选择前先将已被寻访的位置剔除。(一个8x8大小的布尔矩阵是64字节,我们可以用一个double类型的8字节(64位)来表示,通过位操作来改变这个记录)。但由于题目的棋盘范围为8x8,盲目地选择位置搜索仍然会带来不必要的时间耗损。
逐步求精算法描述
一条成功周游的路线,我们在找寻时假设有N个合法的next位置,我们假设所有的next位置会导向死路的概率相同,我们倾向于先搜索可行路径更少的节点,这样就能够及早地发现死路及早回溯。
如图,若在选择next节点前,我们先根据next节点的next节点个数进行升序排序,在通常情况下能够避免在找寻中在错误的路径中耗费太多时间,同时,一条可行的路径在搜索过程中,next节点的个数应该是越来越少的。
我们在position这个数据结构中添加一个变量potential记录这个位置的合法next位置的数目,在选择下一节点前,先通过排序,选择potential更小的节点进行访问。
上面的这个优化思路是可行的。为什么?
维基百科告诉我们,马的周游问题其实就是一个古老的图问题----哈密尔顿路径的一种形式.题目要求寻找的是一条“开路径”(遍历所有位置后不需要回到初始位置)。Cull和Conrad证明了对于任何一个m×n(m≤n且m≥5)棋盘,至少有一个(可能是开路径)的马周游路径。
上面我简单用图表示的现象,十分没有说服力,因为我也没办法确定这样一定正确。事实上,这个想法和Warnsdorff规则不谋而合。
Warnsdorff在1823年提出了一个启发性的贪心算法,我们称为Warnsdorff规则,指在所有可走且未经过的方格中,马只可能走这样一个方格:从该方格出发,马能跳的方格数最少;如果可跳的方格数相等,则从当前位置看,方格序号小的优先。依照这一规则往往可以找到一条路径但是并不一定能够成功。换言之,在进行深搜时优先拓展拥有最少下一步可能移动位置的子节点。
此外,Warnsdorff 算法还有两个改进版本 W+和 W2,但在8 × 8这样小规模的棋盘上
优化效果并不明显。这个问题可以通过分治法和神经网络来解决。
Further Read:Knight's tour - Wikipedia 下面的参考文献
SOJ 1151 魔板
题目描述
SOJ 1151是一道关于搜索的题目,魔板由八个方块组成,为一个2×4的矩阵,每块分别用1-8表示颜色区别,每一次均可以对其进行一次操作,其中可选操作为A,B,C:
A操作(上下行互换)
B操作(每次以行循环右移一个)
C操作(中间四小块顺时针转一格)
魔板初始状态为
算法思想及解题用到的主要数据结构
由于本题的目标是尽快找到解,通过分析,我们可以知道从一个状态执行三种操作到达其下一个状态,在决策树中三个分支是代价一致的(即所有深度相同的节点代价相同),因此我们可以通过广度优先搜索搜寻解,其找到的解必定是最优解。
广度优先搜索的过程我们需要用到队列这种数据结构来辅助。
关于魔板的表示方式,我们可以使用字符串,定义一个结构体board,其中包括两个字符串status和op,status为一个表示此魔板状态的8长字符串,只有字符1-8,op表示初态转换为当前魔板状态的操作序列,由字符ABC组成,初态的op为空字符串。
同时,由于由1-8组成的8串只有8!=40320种不同情况,我们可以想办法记录已经搜索过的状况,确保没有重复搜索。
记录已经搜索状况的数据结构,需要用到关联数组。
详细解题思路
根据广搜的原理,我们首先将目标状态放入队列,对于维护队列的队头,我们先检查其符不符合目标状态,若不符合,我们获得它经过三种操作后的三种状态,放入队尾,然后把当前队头弹出队列。直到我们找到目标状态,或者操作的深度已经超过最大限度,循环结束。
同时为了方便判断重复状态,我们在将状态放入队列之前还需要将其记录下来,以map为例,我们在将下一状态放入队列前,先在map中搜索,判断其是否为已经搜索过的状态,若否,我们将该状态的<status, op>数据对放入用于判断的map中。
逐步求精算法描述
由于在map中搜索也需要一定的时间复杂度,为了避免不必要的搜索,我们可以在插入队列前先做一定的剪枝。
考虑如同XX……XX的一个操作序列/字符串,我们可以知道,一个状态连续进行两次A操作会变为它本身,一个不必搜索的状态,在计算三种操作能到达的状态前,我们可以先分析当前状态的op串的最后一个字符串,若为A,则我们不必搜寻其进行A操作后得到的下一个状态,达到剪枝的目的,并节省需要在map中搜索才得出结果的时间。
同理XX……X = XX……XBBBB,XX……X = XX……XCCCC,可以帮助剪枝。
当然,上面这个方法只是小儿科,当我们能将进行一次操作的复杂度降低时,便不需要上面的这个预分析的办法,下面讲讲两种优化技巧。
康托展开
康托展开是一个全排列到一个自然数的双射,常用于构建哈希表时的空间压缩。康托展开的实质是计算当前排列在所有由小到大全排列中的顺序,因此是可逆的。比如说题目中的这种情况,一个魔板状态相当于一个1到8的全排列状态,通过康托展开,我们可以用一个0 到 40319的数字表示8!种状态,又因为这是一个双射,很容易可以通过这个数字还原这个全排列。
位运算处理
模板状态的保存问题,我们看到题目,很自然会想到用一个2x4的字符矩阵来保存这个状态,又或者是一个大小为8的数组,所以储存一个状态占用8个字节。对于ABC三类操作,通过交换数组/矩阵内的元素位置实现。这里引入位运算的办法来简化这一过程。
8个1-8的十进制数,用二进制表示,每个数至少要4位,一共需要32位(四字节),即一个int类型的大小。我们就用一个int类型内的二进制位表示一个魔板状态。
这样一来,对数组内的元素交换位置,可以改为速度更快的微操作:
A(x) = (x ≪ 16) | (x ≫ 16)
前16位表示第一行,后16位表示第二行,将x左移16位和右移16位的结果合并,则实现上下行的交换
B(x) = [(x &0xFFF0FFF0) ≫ 4] | [(x &0x000F000F) ≪ 12]
(x &0x000F000F),取出魔板的最右一列,左移12位变为左数第一列,将其余的三列((x &0xFFF0FFF0))右移4位,表示循环右移的结果
C(x) = (x &0xF00FF00F) | [(x &0x0F000000) ≫ 4] | [(x &0x00F00000) ≫ 16]
| [(x &0x00000F00) ≪ 16] | [(x &0x000000F0) ≪ 4]
相当于初始状态中2-3-6-7循环交换位置。
这一做法是一个同学的启发,他用位操作用得非常巧妙,经常受他启发。当然很多时候很多问题用位操作都可以加速,只是思考编码的过程如果不熟练的话需要更多的时间。
总结
N为状态总数,在预处理时,广度优先需要访问每个状态,对于每个状态需要O(log N)的时间复杂度。将其插入到关联数组中。在回答输入的查询时,对于每个查询需要O(log N)的时间复杂度来得到关联数组中的元素。假设一共有M个查询,则该算法的时间复杂度为O(Nlog N + Mlog N) = O((N + M) log N)。
简单地说,我们求精的思路过程是:
简单的广搜,没有记忆化(会有很多重复状态)->加入记忆化,记录已经走过的状态(判断一个状态有没有走过也需要时间)->剪枝,通过查看操作序列判断是否应该执行某操作,因若进行该操作,得到的状态必然为已经走过的(判断这个也需要时间)->把所有可能先搜出来并记录,对于每条查询,直接在答案中找。
SOJ 1151是一道关于搜索的题目,魔板由八个方块组成,为一个2×4的矩阵,每块分别用1-8表示颜色区别,每一次均可以对其进行一次操作,其中可选操作为A,B,C:
A操作(上下行互换)
B操作(每次以行循环右移一个)
C操作(中间四小块顺时针转一格)
魔板初始状态为
1 2 3 4
8 7 6 5
给定一个目标状态,给定一个最大步数,要求求出从初态到目标态的最小操作序列,若超出最大步数则停止计算,输出-1算法思想及解题用到的主要数据结构
由于本题的目标是尽快找到解,通过分析,我们可以知道从一个状态执行三种操作到达其下一个状态,在决策树中三个分支是代价一致的(即所有深度相同的节点代价相同),因此我们可以通过广度优先搜索搜寻解,其找到的解必定是最优解。
广度优先搜索的过程我们需要用到队列这种数据结构来辅助。
关于魔板的表示方式,我们可以使用字符串,定义一个结构体board,其中包括两个字符串status和op,status为一个表示此魔板状态的8长字符串,只有字符1-8,op表示初态转换为当前魔板状态的操作序列,由字符ABC组成,初态的op为空字符串。
同时,由于由1-8组成的8串只有8!=40320种不同情况,我们可以想办法记录已经搜索过的状况,确保没有重复搜索。
记录已经搜索状况的数据结构,需要用到关联数组。
详细解题思路
根据广搜的原理,我们首先将目标状态放入队列,对于维护队列的队头,我们先检查其符不符合目标状态,若不符合,我们获得它经过三种操作后的三种状态,放入队尾,然后把当前队头弹出队列。直到我们找到目标状态,或者操作的深度已经超过最大限度,循环结束。
同时为了方便判断重复状态,我们在将状态放入队列之前还需要将其记录下来,以map为例,我们在将下一状态放入队列前,先在map中搜索,判断其是否为已经搜索过的状态,若否,我们将该状态的<status, op>数据对放入用于判断的map中。
逐步求精算法描述
由于在map中搜索也需要一定的时间复杂度,为了避免不必要的搜索,我们可以在插入队列前先做一定的剪枝。
考虑如同XX……XX的一个操作序列/字符串,我们可以知道,一个状态连续进行两次A操作会变为它本身,一个不必搜索的状态,在计算三种操作能到达的状态前,我们可以先分析当前状态的op串的最后一个字符串,若为A,则我们不必搜寻其进行A操作后得到的下一个状态,达到剪枝的目的,并节省需要在map中搜索才得出结果的时间。
同理XX……X = XX……XBBBB,XX……X = XX……XCCCC,可以帮助剪枝。
当然,上面这个方法只是小儿科,当我们能将进行一次操作的复杂度降低时,便不需要上面的这个预分析的办法,下面讲讲两种优化技巧。
康托展开
康托展开是一个全排列到一个自然数的双射,常用于构建哈希表时的空间压缩。康托展开的实质是计算当前排列在所有由小到大全排列中的顺序,因此是可逆的。比如说题目中的这种情况,一个魔板状态相当于一个1到8的全排列状态,通过康托展开,我们可以用一个0 到 40319的数字表示8!种状态,又因为这是一个双射,很容易可以通过这个数字还原这个全排列。
位运算处理
模板状态的保存问题,我们看到题目,很自然会想到用一个2x4的字符矩阵来保存这个状态,又或者是一个大小为8的数组,所以储存一个状态占用8个字节。对于ABC三类操作,通过交换数组/矩阵内的元素位置实现。这里引入位运算的办法来简化这一过程。
8个1-8的十进制数,用二进制表示,每个数至少要4位,一共需要32位(四字节),即一个int类型的大小。我们就用一个int类型内的二进制位表示一个魔板状态。
这样一来,对数组内的元素交换位置,可以改为速度更快的微操作:
A(x) = (x ≪ 16) | (x ≫ 16)
前16位表示第一行,后16位表示第二行,将x左移16位和右移16位的结果合并,则实现上下行的交换
B(x) = [(x &0xFFF0FFF0) ≫ 4] | [(x &0x000F000F) ≪ 12]
(x &0x000F000F),取出魔板的最右一列,左移12位变为左数第一列,将其余的三列((x &0xFFF0FFF0))右移4位,表示循环右移的结果
C(x) = (x &0xF00FF00F) | [(x &0x0F000000) ≫ 4] | [(x &0x00F00000) ≫ 16]
| [(x &0x00000F00) ≪ 16] | [(x &0x000000F0) ≪ 4]
相当于初始状态中2-3-6-7循环交换位置。
这一做法是一个同学的启发,他用位操作用得非常巧妙,经常受他启发。当然很多时候很多问题用位操作都可以加速,只是思考编码的过程如果不熟练的话需要更多的时间。
总结
N为状态总数,在预处理时,广度优先需要访问每个状态,对于每个状态需要O(log N)的时间复杂度。将其插入到关联数组中。在回答输入的查询时,对于每个查询需要O(log N)的时间复杂度来得到关联数组中的元素。假设一共有M个查询,则该算法的时间复杂度为O(Nlog N + Mlog N) = O((N + M) log N)。
简单地说,我们求精的思路过程是:
简单的广搜,没有记忆化(会有很多重复状态)->加入记忆化,记录已经走过的状态(判断一个状态有没有走过也需要时间)->剪枝,通过查看操作序列判断是否应该执行某操作,因若进行该操作,得到的状态必然为已经走过的(判断这个也需要时间)->把所有可能先搜出来并记录,对于每条查询,直接在答案中找。
2014年12月11日星期四
ID3决策树算法笔记及一个简单应用
机器学习中的决策树训练,使用决策树作为预测模型来预测样本的类标。这种决策树也称作分类树(当属性为离散值)或回归树(当属性为连续值)。名词分类与回归树(Classification And Regression Tree,CART)指的便是这一统称。很自然我们可以想到,在更复杂的情况下,若属性的集合中既包括离散值的属性,也包括连续值的方向,两种树需要被结合。在这些树的结构里, 叶子节点给出的是最终的决策值,而从根节点到叶节点的过程,表示的是从一开始的整个决策属性选择过程。下面我通过人工智能课程作业的样例来对离散情况下的分类树算法进行简介。
例:给定一组美国国会的投票结果数据集,若根据一个人对各类议题的态度推断出其党派。需要通过划分用一部分数据训练出决策树。这棵决策树的准确率我们可以用另一部分数据进行准确度检验。
数据来源:1984 United States Congressional Voting Records Database
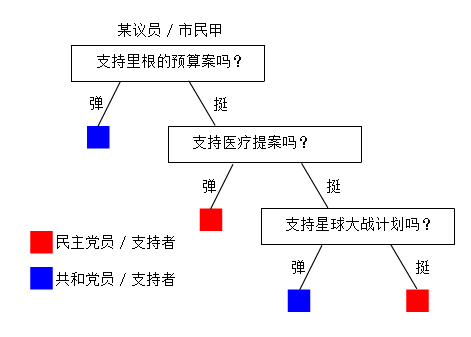
没了解过的人,大概也能看懂下面这幅图,在1984年美国某个社会调查小组也许会通过总结社调结果搞出类似这样一个东西,当然这个我是瞎掰的:
决策树便是利用一些统计学的知识,利用已有的信息,帮助对未知的信息进行决策。我们当然希望这样一个过程越短越好,越准确越好。
数据模型
将数据集的每条记录视作一个数据结构,训练集中,每一条记录都有其所属党派,可以分为共和党(下称Rep)或民主党(下称Dem)。数据中每一个议员都在十六个不同的议题上表态,我们将这十六个议题视作这条数据记录的十六个属性。在这个问题上,每个属性都有三个可能取值:Yes,No,Unknown,表示投票结果的三种可能。
评估模型
为了最小化决策树深度,我们需要每次尽量挑选能最好划分数据集的属性。理想情况下是能将样例分为只包括正或反例的子数据集。最糟糕的情况是划出的子数据集中正反例的数量比例一致。
为什么要这样做?简单画了这个示意图,我想可以说明选择属性的重要性。
民主党的人大概会更倾向于反对时任共和党总统里根的预算案,这是一个区分度高的议题,但援助尼加拉瓜反政府军这个问题很可能一个党内意见就未必那么统一(上面这图也是我瞎掰的,因为在数据中发现,即使是一些看上去区分度应该很低的议题,同一个党内的意见统一度也很高)。再举个离谱点的例子,对于一个中原人,他喜欢吃咸豆腐脑还是甜豆腐花,更多地可能可以用来判断他是南方人还是北方人,而不是他属于左派还是右派。也就是说,如果我们好的议题作为第一个划分的依据,很可能很快就结束整个决策树的建造。
我们引入一个函数I评估一组数据能提供的期望信息量。
当这组数据中正反两例的比例越接近的时候,函数的值越接近1,而数据的比例越悬殊,函数值越接近0。
对于一个特定属性A,我们评估选择其作为划分属性时所能获得的增益,需要函数:
其中对于属性A中的属性值a1,a2,…,an(在这个样例中为Yes,No,Unknown),我们需计算:
Remainder用于评估选择该属性后能获得的信息量,我们希望根据这个属性划分后的子数据集中,党派的分散程度越小越好(即能更快完成划分),因此我们计算根据此属性划分后其子数据集的信息量加权和。这个值越小,即说明划分后各子数据集的党派集中度越高。信息增益即为原始数据的信息量和划分后的信息量的差值。
算法分析
决策树的训练过程是通过对原始数据集的属性进行分类(归纳学习),在这个问题上我们讨论布尔分类,即只有正反两个值的离散函数。假定对于一个议员m,其所属党派是一个关于其在十六个议题上投票意向的布尔函数,我们需要根据训练集训练出如下函数,也就是类似第一张图展示的结果:
对于训练集中的所有记录,我们需要决定用哪个属性来进行树的训练。例如我们选择议题一(下称属性)作为划分标准后,便可以根据各条记录在这个属性上所取的值,将数据集划分为三组,将这些数据集分配给当前树节点的三个子节点,我们便可以递归地进行这个过程。一个决策树节点在递归过程中,在一定条件下成为叶子节点,即最终对应决策值的决策节点,此时递归停止。
算法流程
A.对于每个节点的训练过程,若该节点的数据集中同时存在Rep与Dem,我们继续选择一个属性,来对这个节点进行进一步划分;
B.若数据集中均为Rep或均为Dem,这个节点已可视为完成,可以根据数据集中剩余的是Rep还是Dem来决定这个节点的决策;
C.当一个节点被划分到一个没有任何实例的情况,其训练集为空时,说明在其父节点的数据集中,对于其父节点所选取的属性,并没有任何一条取了当前节点对应的属性值。这种情况我们同样需要视为完成,这个节点的决策缺省值应该由其父节点来决定;
D.由于决策树中,每一条从根节点到叶子节点(决策节点)的路径中,中间节点所选择的属性不能出现重复,当一条路径已经用完全部属性后,我们将面临噪声的问题。换言之,当前的训练集实例中,有完全相同的属性描述,但却取了不同的正反值(即有分属两党的议员在所有议题上的态度都吻合)。我们在这里选取的办法是取数据集中的大多数作为这个决策节点的决策值。
伪代码
算法优化
在有大规模属性集的情况下,在数据中寻找无意义的规律性,这种情况称为过拟合。 为了避免在训练过程中噪声的出现产生过拟合,我们需要尽量避免引入无关的属性(如 下图所示)。一种办法是改变终止递归的条件以实现剪枝。引入信息量函数后,我们可以在处理每个节点的时候先计算其训练集的信息量函数,若信息量小到不足以让我们对 其进行进一步划分(这种情况下,训练集中的正反例比例将非常不平衡,最极端的情况下,只有正例或只有反例时信息量为0),我们则不需要等到样例中只剩同一种样本,而是直接停止递归,用样本中的多数值作为此叶子节点的决策值。
我们需要做的便是,将伪代码中
else if attributes is empty //已无属性可划分
return PLURALITY-VALUE(examples) //返回样例的多数值
改为
else if the choosed best attribute’s I < threshold //属性的增益小于阈值
return PLURALITY-VALUE(examples) //返回样例的多数值
对于一个有噪声的数据集,这个方法很有用。阈值取什么是关键,我们通过多个阈值的十折交叉测试,发现一个有趣的现象,对于这个样例而言最佳的阈值有两段,而不是像想像中那样只有一个峰值。这个现象的原因未明。
例:给定一组美国国会的投票结果数据集,若根据一个人对各类议题的态度推断出其党派。需要通过划分用一部分数据训练出决策树。这棵决策树的准确率我们可以用另一部分数据进行准确度检验。
数据来源:1984 United States Congressional Voting Records Database
没了解过的人,大概也能看懂下面这幅图,在1984年美国某个社会调查小组也许会通过总结社调结果搞出类似这样一个东西,当然这个我是瞎掰的:
决策树便是利用一些统计学的知识,利用已有的信息,帮助对未知的信息进行决策。我们当然希望这样一个过程越短越好,越准确越好。
数据模型
将数据集的每条记录视作一个数据结构,训练集中,每一条记录都有其所属党派,可以分为共和党(下称Rep)或民主党(下称Dem)。数据中每一个议员都在十六个不同的议题上表态,我们将这十六个议题视作这条数据记录的十六个属性。在这个问题上,每个属性都有三个可能取值:Yes,No,Unknown,表示投票结果的三种可能。
评估模型
为了最小化决策树深度,我们需要每次尽量挑选能最好划分数据集的属性。理想情况下是能将样例分为只包括正或反例的子数据集。最糟糕的情况是划出的子数据集中正反例的数量比例一致。
为什么要这样做?简单画了这个示意图,我想可以说明选择属性的重要性。
民主党的人大概会更倾向于反对时任共和党总统里根的预算案,这是一个区分度高的议题,但援助尼加拉瓜反政府军这个问题很可能一个党内意见就未必那么统一(上面这图也是我瞎掰的,因为在数据中发现,即使是一些看上去区分度应该很低的议题,同一个党内的意见统一度也很高)。再举个离谱点的例子,对于一个中原人,他喜欢吃咸豆腐脑还是甜豆腐花,更多地可能可以用来判断他是南方人还是北方人,而不是他属于左派还是右派。也就是说,如果我们好的议题作为第一个划分的依据,很可能很快就结束整个决策树的建造。
我们引入一个函数I评估一组数据能提供的期望信息量。
当这组数据中正反两例的比例越接近的时候,函数的值越接近1,而数据的比例越悬殊,函数值越接近0。
对于一个特定属性A,我们评估选择其作为划分属性时所能获得的增益,需要函数:
其中对于属性A中的属性值a1,a2,…,an(在这个样例中为Yes,No,Unknown),我们需计算:
Remainder用于评估选择该属性后能获得的信息量,我们希望根据这个属性划分后的子数据集中,党派的分散程度越小越好(即能更快完成划分),因此我们计算根据此属性划分后其子数据集的信息量加权和。这个值越小,即说明划分后各子数据集的党派集中度越高。信息增益即为原始数据的信息量和划分后的信息量的差值。
算法分析
决策树的训练过程是通过对原始数据集的属性进行分类(归纳学习),在这个问题上我们讨论布尔分类,即只有正反两个值的离散函数。假定对于一个议员m,其所属党派是一个关于其在十六个议题上投票意向的布尔函数,我们需要根据训练集训练出如下函数,也就是类似第一张图展示的结果:
对于训练集中的所有记录,我们需要决定用哪个属性来进行树的训练。例如我们选择议题一(下称属性)作为划分标准后,便可以根据各条记录在这个属性上所取的值,将数据集划分为三组,将这些数据集分配给当前树节点的三个子节点,我们便可以递归地进行这个过程。一个决策树节点在递归过程中,在一定条件下成为叶子节点,即最终对应决策值的决策节点,此时递归停止。
算法流程
A.对于每个节点的训练过程,若该节点的数据集中同时存在Rep与Dem,我们继续选择一个属性,来对这个节点进行进一步划分;
B.若数据集中均为Rep或均为Dem,这个节点已可视为完成,可以根据数据集中剩余的是Rep还是Dem来决定这个节点的决策;
C.当一个节点被划分到一个没有任何实例的情况,其训练集为空时,说明在其父节点的数据集中,对于其父节点所选取的属性,并没有任何一条取了当前节点对应的属性值。这种情况我们同样需要视为完成,这个节点的决策缺省值应该由其父节点来决定;
D.由于决策树中,每一条从根节点到叶子节点(决策节点)的路径中,中间节点所选择的属性不能出现重复,当一条路径已经用完全部属性后,我们将面临噪声的问题。换言之,当前的训练集实例中,有完全相同的属性描述,但却取了不同的正反值(即有分属两党的议员在所有议题上的态度都吻合)。我们在这里选取的办法是取数据集中的大多数作为这个决策节点的决策值。
伪代码
function DECISION-TREE-LEARNING(examples, attributes, parent_examples) returns a tree
if examples is empty //当前节点样例集若为空
return PLURALITY-VALUE(parent_examples) //返回父节点的多数值
else if examples have the same classification //样例集清一色相同
return the classification //返回该分类值
else if attributes is empty //已无属性可划分
return PLURALITY-VALUE(examples) //返回样例的多数值
else //需要递归建树
A ß ArgMax(IMPORTANCE(a, examples)) //选出最佳属性
tree ß a new decision tree with root test A
for each value vk of A do //为子节点分配样例
exs ß {e : e ∈ examples and e.A = Vk}
subtree ß DECISION-TREE-LEARNING(exs,atrributes-A,examples)
add a branch to tree with label (A = Vk) and sub-tree subtree
return tree
算法优化
在有大规模属性集的情况下,在数据中寻找无意义的规律性,这种情况称为过拟合。 为了避免在训练过程中噪声的出现产生过拟合,我们需要尽量避免引入无关的属性(如 下图所示)。一种办法是改变终止递归的条件以实现剪枝。引入信息量函数后,我们可以在处理每个节点的时候先计算其训练集的信息量函数,若信息量小到不足以让我们对 其进行进一步划分(这种情况下,训练集中的正反例比例将非常不平衡,最极端的情况下,只有正例或只有反例时信息量为0),我们则不需要等到样例中只剩同一种样本,而是直接停止递归,用样本中的多数值作为此叶子节点的决策值。
我们需要做的便是,将伪代码中
else if attributes is empty //已无属性可划分
return PLURALITY-VALUE(examples) //返回样例的多数值
改为
else if the choosed best attribute’s I < threshold //属性的增益小于阈值
return PLURALITY-VALUE(examples) //返回样例的多数值
对于一个有噪声的数据集,这个方法很有用。阈值取什么是关键,我们通过多个阈值的十折交叉测试,发现一个有趣的现象,对于这个样例而言最佳的阈值有两段,而不是像想像中那样只有一个峰值。这个现象的原因未明。
订阅:
博文
(
Atom
)