例:给定一组美国国会的投票结果数据集,若根据一个人对各类议题的态度推断出其党派。需要通过划分用一部分数据训练出决策树。这棵决策树的准确率我们可以用另一部分数据进行准确度检验。
数据来源:1984 United States Congressional Voting Records Database
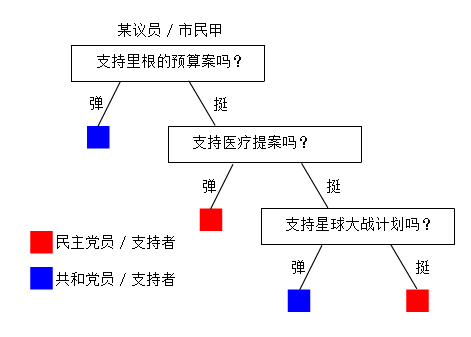
没了解过的人,大概也能看懂下面这幅图,在1984年美国某个社会调查小组也许会通过总结社调结果搞出类似这样一个东西,当然这个我是瞎掰的:
决策树便是利用一些统计学的知识,利用已有的信息,帮助对未知的信息进行决策。我们当然希望这样一个过程越短越好,越准确越好。
数据模型
将数据集的每条记录视作一个数据结构,训练集中,每一条记录都有其所属党派,可以分为共和党(下称Rep)或民主党(下称Dem)。数据中每一个议员都在十六个不同的议题上表态,我们将这十六个议题视作这条数据记录的十六个属性。在这个问题上,每个属性都有三个可能取值:Yes,No,Unknown,表示投票结果的三种可能。
评估模型
为了最小化决策树深度,我们需要每次尽量挑选能最好划分数据集的属性。理想情况下是能将样例分为只包括正或反例的子数据集。最糟糕的情况是划出的子数据集中正反例的数量比例一致。
为什么要这样做?简单画了这个示意图,我想可以说明选择属性的重要性。
民主党的人大概会更倾向于反对时任共和党总统里根的预算案,这是一个区分度高的议题,但援助尼加拉瓜反政府军这个问题很可能一个党内意见就未必那么统一(上面这图也是我瞎掰的,因为在数据中发现,即使是一些看上去区分度应该很低的议题,同一个党内的意见统一度也很高)。再举个离谱点的例子,对于一个中原人,他喜欢吃咸豆腐脑还是甜豆腐花,更多地可能可以用来判断他是南方人还是北方人,而不是他属于左派还是右派。也就是说,如果我们好的议题作为第一个划分的依据,很可能很快就结束整个决策树的建造。
我们引入一个函数I评估一组数据能提供的期望信息量。
当这组数据中正反两例的比例越接近的时候,函数的值越接近1,而数据的比例越悬殊,函数值越接近0。
对于一个特定属性A,我们评估选择其作为划分属性时所能获得的增益,需要函数:
其中对于属性A中的属性值a1,a2,…,an(在这个样例中为Yes,No,Unknown),我们需计算:
Remainder用于评估选择该属性后能获得的信息量,我们希望根据这个属性划分后的子数据集中,党派的分散程度越小越好(即能更快完成划分),因此我们计算根据此属性划分后其子数据集的信息量加权和。这个值越小,即说明划分后各子数据集的党派集中度越高。信息增益即为原始数据的信息量和划分后的信息量的差值。
算法分析
决策树的训练过程是通过对原始数据集的属性进行分类(归纳学习),在这个问题上我们讨论布尔分类,即只有正反两个值的离散函数。假定对于一个议员m,其所属党派是一个关于其在十六个议题上投票意向的布尔函数,我们需要根据训练集训练出如下函数,也就是类似第一张图展示的结果:
对于训练集中的所有记录,我们需要决定用哪个属性来进行树的训练。例如我们选择议题一(下称属性)作为划分标准后,便可以根据各条记录在这个属性上所取的值,将数据集划分为三组,将这些数据集分配给当前树节点的三个子节点,我们便可以递归地进行这个过程。一个决策树节点在递归过程中,在一定条件下成为叶子节点,即最终对应决策值的决策节点,此时递归停止。
算法流程
A.对于每个节点的训练过程,若该节点的数据集中同时存在Rep与Dem,我们继续选择一个属性,来对这个节点进行进一步划分;
B.若数据集中均为Rep或均为Dem,这个节点已可视为完成,可以根据数据集中剩余的是Rep还是Dem来决定这个节点的决策;
C.当一个节点被划分到一个没有任何实例的情况,其训练集为空时,说明在其父节点的数据集中,对于其父节点所选取的属性,并没有任何一条取了当前节点对应的属性值。这种情况我们同样需要视为完成,这个节点的决策缺省值应该由其父节点来决定;
D.由于决策树中,每一条从根节点到叶子节点(决策节点)的路径中,中间节点所选择的属性不能出现重复,当一条路径已经用完全部属性后,我们将面临噪声的问题。换言之,当前的训练集实例中,有完全相同的属性描述,但却取了不同的正反值(即有分属两党的议员在所有议题上的态度都吻合)。我们在这里选取的办法是取数据集中的大多数作为这个决策节点的决策值。
伪代码
function DECISION-TREE-LEARNING(examples, attributes, parent_examples) returns a tree
if examples is empty //当前节点样例集若为空
return PLURALITY-VALUE(parent_examples) //返回父节点的多数值
else if examples have the same classification //样例集清一色相同
return the classification //返回该分类值
else if attributes is empty //已无属性可划分
return PLURALITY-VALUE(examples) //返回样例的多数值
else //需要递归建树
A ß ArgMax(IMPORTANCE(a, examples)) //选出最佳属性
tree ß a new decision tree with root test A
for each value vk of A do //为子节点分配样例
exs ß {e : e ∈ examples and e.A = Vk}
subtree ß DECISION-TREE-LEARNING(exs,atrributes-A,examples)
add a branch to tree with label (A = Vk) and sub-tree subtree
return tree
算法优化
在有大规模属性集的情况下,在数据中寻找无意义的规律性,这种情况称为过拟合。 为了避免在训练过程中噪声的出现产生过拟合,我们需要尽量避免引入无关的属性(如 下图所示)。一种办法是改变终止递归的条件以实现剪枝。引入信息量函数后,我们可以在处理每个节点的时候先计算其训练集的信息量函数,若信息量小到不足以让我们对 其进行进一步划分(这种情况下,训练集中的正反例比例将非常不平衡,最极端的情况下,只有正例或只有反例时信息量为0),我们则不需要等到样例中只剩同一种样本,而是直接停止递归,用样本中的多数值作为此叶子节点的决策值。
我们需要做的便是,将伪代码中
else if attributes is empty //已无属性可划分
return PLURALITY-VALUE(examples) //返回样例的多数值
改为
else if the choosed best attribute’s I < threshold //属性的增益小于阈值
return PLURALITY-VALUE(examples) //返回样例的多数值
对于一个有噪声的数据集,这个方法很有用。阈值取什么是关键,我们通过多个阈值的十折交叉测试,发现一个有趣的现象,对于这个样例而言最佳的阈值有两段,而不是像想像中那样只有一个峰值。这个现象的原因未明。

没有评论 :
发表评论